AcWing蓝桥杯辅导课：第一讲递推与递归

news/2025/2/27 6:55:25

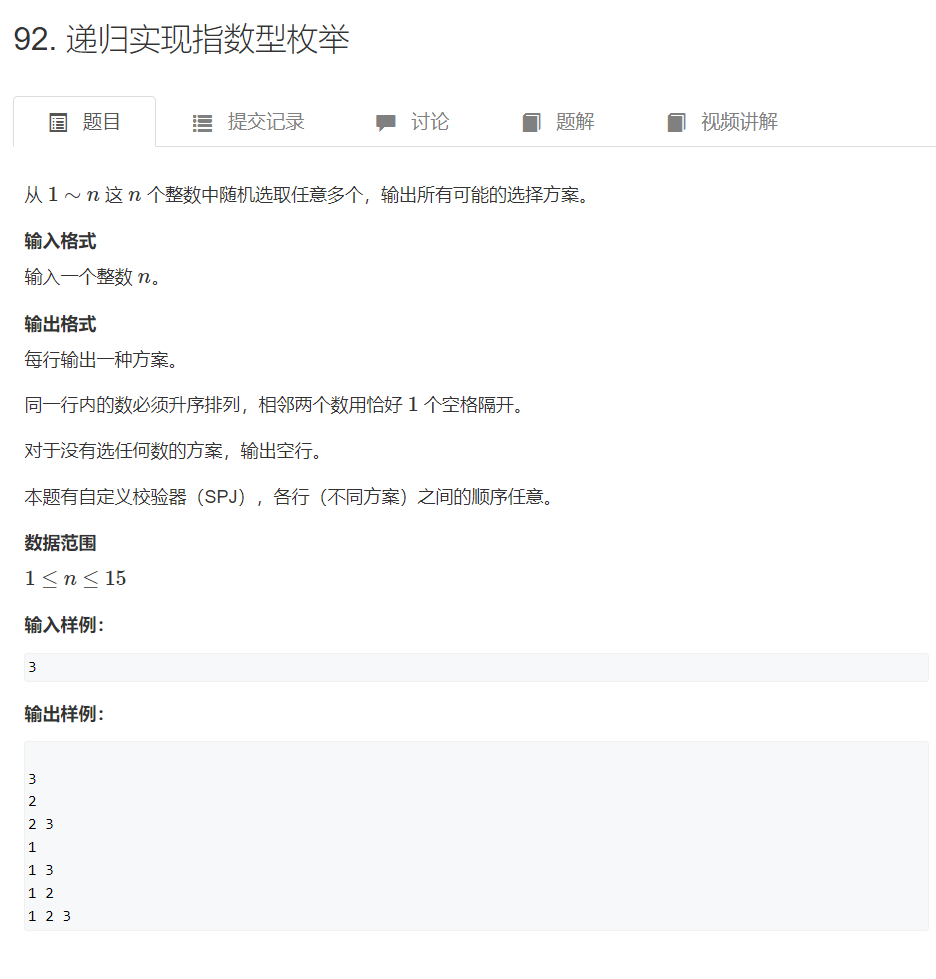
AcWing 92. 递归实现指数型枚举

在这里插入图片描述
思路：

方法一： 暴力枚举

用二进制加位运算枚举每一个状态，输出即可，时间复杂度为 O ( N 2 N ) O(N2^N) O(N2N)

代码：

java">import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/22 11:08
 */
public class Main {
    static Scanner scanner = new Scanner(System.in);
    static int n;

    public static void main(String[] args) {
        n = scanner.nextInt();
        for (int i = 0; i < (1 << n); i++) {
            for (int j = 0; j < n; j++) {
                if (((i >> j) & 1) == 1) {
                    System.out.print((j + 1) + " ");
                }
            }
            System.out.println();
        }
    }

}

方法二： 深搜

用一个数组存储每个数字的状态， 0表示不放， 1表示放，如果当前状态是1的话，就输出该数，与求全排列代码类似。

java">import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/22 11:08
 */
public class Main {
    static Scanner scanner = new Scanner(System.in);
    static final int N = 20;
    static int n;
    // 0不选 1选
    static int[] st = new int[N];

    public static void main(String[] args) {
        n = scanner.nextInt();
        dfs(1);
    }

    public static void dfs(int u) {
        if (u == n + 1) {
            for (int i = 1; i <= n; i++) {
                if (st[i] == 1) System.out.print(i + " ");
            }
            System.out.println();
            return;
        }

        st[u] = 0;
        dfs(u + 1);
        st[u] = 1;
        dfs(u + 1);
    }

}

AcWing 94. 递归实现排列型枚举

在这里插入图片描述
思路：
深度优先搜索，时间复杂度为 O ( N ∗ N ! ) O(N*N!) O(N∗N!)，注意Java 的 System.out.println() 输出效率低， 本题会超时，所以用 BufferedWrite 来输出。

代码：

java">import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/22 10:25
 */
public class Main {
    static final int N = 15;
    static int n;
    static boolean[] st = new boolean[N];
    static int[] a = new int[N];
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));

    public static void main(String[] args) throws IOException {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        dfs(0);
        out.flush();
    }

    public static void dfs(int step) throws IOException {
        if (step == n) {
            for (int i = 0; i < n; i++)
                out.write(a[i] + " ");
            out.write('\n');
        } else {
            for (int i = 1; i <= n; i++) {
                if (!st[i]) {
                    a[step] = i;
                    st[i] = true;
                    dfs(step + 1);
                    st[i] = false;
                }
            }
        }
    }
}

AcWing 717. 简单斐波那契

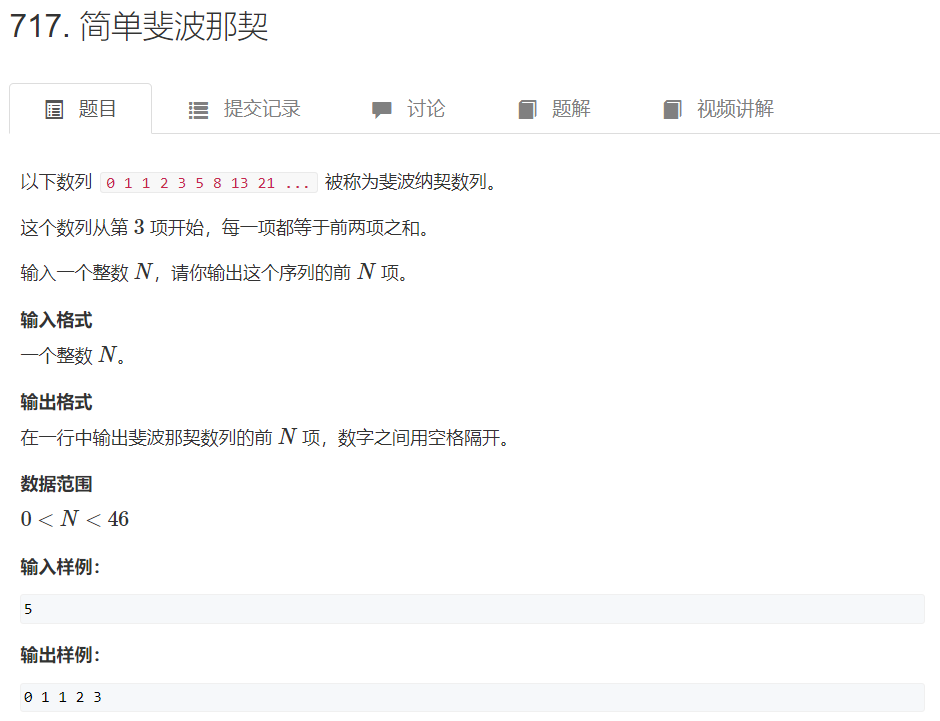
在这里插入图片描述
代码：

java">import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/22 10:43
 */
public class Main {
    static Scanner scanner = new Scanner(System.in);
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    static final int N = 50;
    static int[] fi = new int[N];
    static int n;

    public static void main(String[] args) throws IOException {
        n = scanner.nextInt();
        fi[1] = 0;
        fi[2] = 1;
        for (int i = 3; i <= n; i++) {
            fi[i] = fi[i - 1] + fi[i - 2];
        }
        for (int i = 1; i <= n; i++) {
            out.write(fi[i] + " ");
        }
        out.flush();
    }
}

AcWing 95. 费解的开关

在这里插入图片描述

思路：

考虑第一行，有 2 n 2 ^ n 2n 种不同的状态。对于第一行的每个灯的状态，由于每个开关状态的改变会影响上下左右的所有开关的状态，所以在第一行，如果某灯是灭的话，有且仅有该灯下面第二行的开关的改变能影响该灯的状态，也就是说，只有正下方的开关可以改变上一层的状态，第 n n n 行 确定 n + 1 n + 1 n+1 行的状态，第一行确定整个的状态，所以只需要用二进制枚举第一行的状态即可，判断最后一行是否都为亮的，如果都是亮的，则有可行解，再判断可行解与 6 的 关系。

为保证不同的操作方式之间的结果不干扰，一开始要对原始数组先备份，然后再还原。

代码：

java">import java.util.Arrays;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 15:46
 */
public class Main {

    static final int N = 6;
    static char[][] g = new char[N][N], backup = new char[N][N];
    static int n;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();

        while (n-- != 0) {

            for (int i = 0; i < 5; i++) {
                String s = scanner.next();
                g[i] = s.toCharArray();
            }

            int res = 10;


            for (int op = 0; op < (1 << 5); op++) {

                for (int j = 0; j < 5; j++) {
                    backup[j] = Arrays.copyOf(g[j], 5);
                }

                int step = 0;

                for (int i = 0; i < 5; i++) {
                    if ((op >> i & 1) == 1) {
                        step++;
                        turn(0, i);
                    }
                }

                for (int i = 0; i < 4; i++) {
                    for (int j = 0; j < 5; j++) {
                        if (g[i][j] == '0') {
                            step++;
                            turn(i + 1, j);
                        }
                    }
                }
                boolean flag = false;

                for (int i = 0; i < 5; i++) {
                    if (g[4][i] == '0') {
                        flag = true;
                        break;
                    }
                }

                if (!flag) res = Math.min(res, step);
                for (int j = 0; j < 5; j++) {
                    g[j] = Arrays.copyOf(backup[j], 5);
                }

            }

            if (res > 6) System.out.println(-1);
            else System.out.println(res);
        }

    }


    public static void turn(int x, int y) {
        int[] dx = {-1, 1, 0, 0, 0}, dy = {0, 0, -1, 1, 0};

        for (int i = 0; i < 5; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= 5 || b < 0 || b >= 5) continue;
            g[a][b] ^= 1;
        }
    }
}

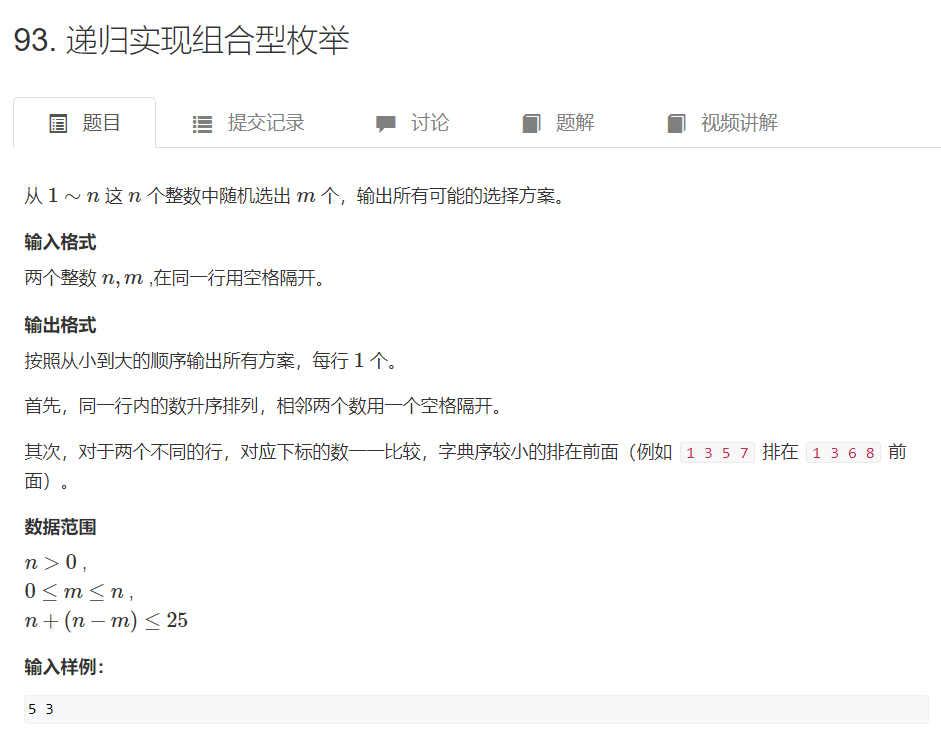
AcWing 93. 递归实现组合型枚举

在这里插入图片描述
思路：

搜索一个数，然后搜索下一个比该数大的数。

剪枝条件： 设当前搜索的是 第 u u u 个数，则已经有了 u − 1 u - 1 u−1 个数，搜索到了 s t a r t start start ，一共有 n n n 个数，还剩 n − s t a r t + 1 n - start + 1 n−start+1 个数。

如果 u − 1 + n − s t a r t + 1 < m u - 1 + n - start + 1 \lt m u−1+n−start+1<m，凑不齐 m m m 个数的组合，就剪去该分支。

代码：

java">import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/22 14:38
 */
public class Main {
    static final int N = 30;
    static int n, m;
    static int[] a = new int[N];
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));

    public static void main(String[] args) throws IOException {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();

        dfs(1, 1);
        out.flush();
    }

    public static void dfs(int step, int start) throws IOException {
        if (step + n - start < m) return;
        if (step == m + 1) {
            for (int i = 1; i <= m; i++)
                out.write(a[i] + " ");
            out.write('\n');
        } else {
            for (int i = start; i <= n; i++) {
                a[step] = i;
                dfs(step + 1, i + 1);
            }
        }
    }
}

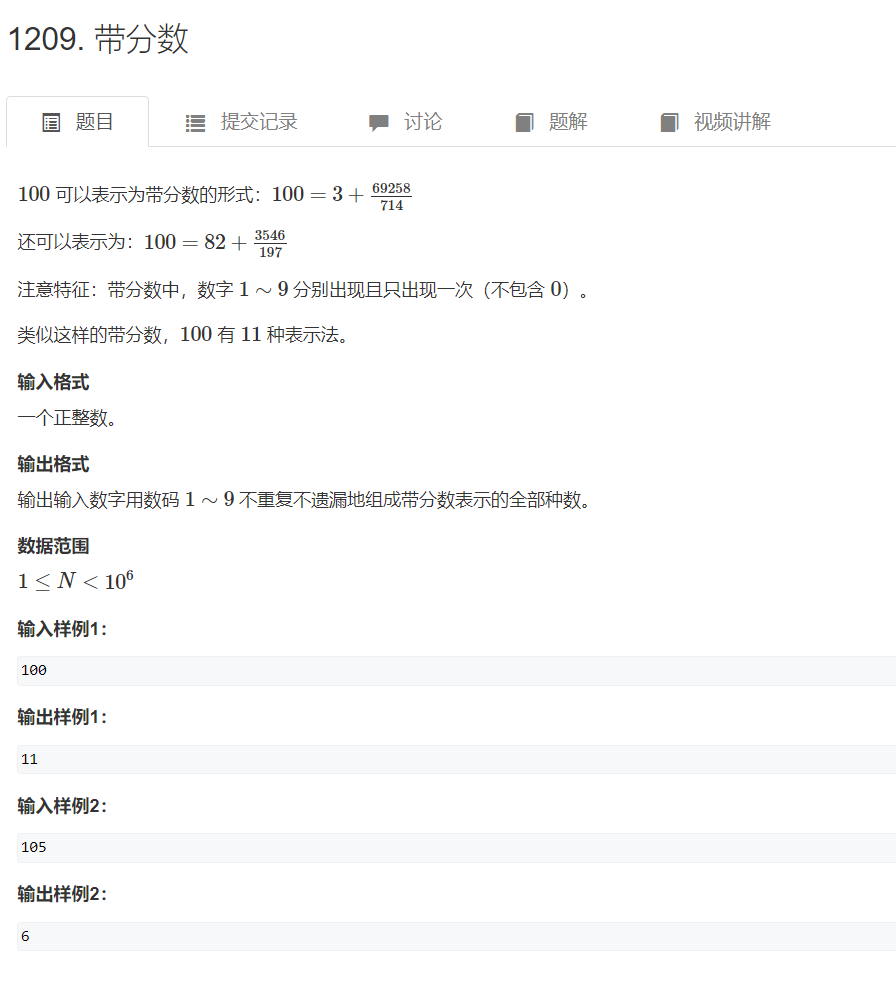
AcWing 1209. 带分数

在这里插入图片描述
思路：

方法一： 暴力枚举全排列，枚举 a a a, b b b , c c c。枚举 a a a, b b b , c c c过程中配以剪枝， a a a的位数不超过6位。

代码：

java">import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 10:08
 */
public class Main {
    static final int N = 15;
    static int ans;
    static int n;
    static int[] arr = new int[N];
    static boolean[] st = new boolean[N];
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        dfs(1);
        System.out.println(ans);
    }

    public static int cal(int a, int b) {
        int sum = 0;

        for (int i = a; i <= b; i++) sum = sum * 10 + arr[i];

        return sum;
    }

    public static void dfs(int u) {
        if (u > 9) {
        // 枚举a, b, c
            for (int i = 1; i <= 6; i++) {
                for (int j = i + 1; j <= 8; j++) {
                    int a = cal(1, i);
                    int b = cal(i + 1, j);
                    int c = cal(j + 1, 9);
                    if (a * c + b == n * c) ans++;
                }
            }

            return;
        }
        for (int i = 1; i <= 9; i++) {
            if (!st[i]) {
                arr[u] = i;
                st[i] = true;
                dfs(u + 1);
                st[i] = false;
            }
        }
    }
}

方法二： 枚举 a a a, c c c。计算 b b b ，判断该组合是否不重不漏用完 1 ∼ 9 1\sim 9 1∼9 中的所有数。

代码：

java">import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 14:27
 */
public class Main {

    static final int N = 15;
    static boolean[] st = new boolean[N], backup = new boolean[N];
    static int n, ans;

    public static void main(String[] args) throws IOException {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        dfs_a(0, 0);
        System.out.println(ans);
    }

    public static void dfs_a(int u, int a) {
    	// 如果 a >= n 不满足条件 剪枝
        if (a >= n) return;
        // 在 a的基础上枚举c
        if (a != 0) dfs_c(u, a, 0);

        for (int i = 1; i <= 9; i++) {
            if (!st[i]) {
                st[i] = true;
                dfs_a(u + 1, a * 10 + i);
                st[i] = false;
            }
        }
    }

    public static void dfs_c(int u, int a, int c) {
        if (u > 9) return;
        if (check(a, c)) ans++;
        for (int i = 1; i <= 9; i++) {
            if (!st[i]) {
                st[i] = true;
                dfs_c(u + 1, a, c * 10 + i);
                st[i] = false;
            }
        }
    }

    public static boolean check(int a, int c) {
    	// 防止爆 int
        long b = n * (long) c - (long)a * c;
        if (a * b * c == 0) return false;
        for (int i = 1; i <= 9; i++) {
            backup[i] = st[i];
        }

        while (b != 0) {
            long x = b % 10;
            b /= 10;
            // 出现了0 或者b的数字与 a c 的有重复 不满足条件
            if (x == 0 || backup[(int)x]) return false;
            backup[(int)x] = true;
        }

		// 保证每个数字都用过了
        for (int i = 1; i <= 9; i++) {
            if (!backup[i]) return false;
        }

        return true;
    }
}

AcWing 116. 飞行员兄弟

在这里插入图片描述
思路：

因为本题规模不大，所以可以通过枚举和位运算来求解，一共有 16 个位置，则有 2 16 = 65536 2^{16} = 65536 216=65536 种状态，最后判断开关的状态。用ArrayList 来存储操作，仅当操作数更少的时候，才更新操作集。

代码：

java">import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 16:48
 */
public class Main {
    static final int N = 5;
    static char[][] g = new char[N][N], backup = new char[N][N];

    static class Node {
        int x, y;

        Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        ArrayList<Node> ans = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            String s = scanner.next();
            g[i] = s.toCharArray();
        }

        for (int op = 0; op < (1 << 16); op++) {

            for (int j = 0; j < 4; j++) {
                backup[j] = Arrays.copyOf(g[j], g[j].length);
            }

            ArrayList<Node> tmp = new ArrayList<>();


            for (int i = 0; i < 4; i++) {
                for (int j = 0; j < 4; j++) {
                    if (((op >> (i * 4 + j)) & 1) == 1) {
                        turn(i, j);
                        tmp.add(new Node(i, j));
                    }
                }
            }

            boolean flag = false;
            for (int i = 0; i < 4; i++) {
                for (int j = 0; j < 4; j++) {
                    if (g[i][j] == '+') {
                        flag = true;
                        break;
                    }
                }
            }

            if (!flag) {
                if (ans.isEmpty() || ans.size() > tmp.size()) ans = tmp;
            }

            for (int j = 0; j < 4; j++) {
                g[j] = Arrays.copyOf(backup[j], backup[j].length);
            }

        }

        System.out.println(ans.size());
        for (Node tmp : ans) {
            System.out.println((tmp.x + 1) + " " + (tmp.y + 1));
        }

    }

    public static void turn(int x, int y) {
        for (int i = 0; i < 4; i++) {
            g[x][i] = g[x][i] == '+' ? '-' : '+';
            g[i][y] = g[i][y] == '+' ? '-' : '+';
        }
        g[x][y] = g[x][y] == '+' ? '-' : '+';

    }
}

AcWing 1208. 翻硬币

在这里插入图片描述
思路：

本题有不超过100个元素，枚举状态会超时，可以考虑贪心来做，如果两个字符串某个相同位置的元素不相同，就翻转，操作的次数就加一。这样只需要用到 O ( N ) O(N) O(N) 的时间复杂度。

代码：

java">import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/24 9:54
 */
public class Main {
    static final int N = 105;
    static char[] s1 = new char[N], s2 = new char[N];
    static String start, end;
    static int n, ans;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        start = scanner.next();
        end = scanner.next();
        n = start.length();
        s1 = start.toCharArray();
        s2 = end.toCharArray();

        for (int i = 0; i < n - 1; i++) {
            if (s1[i] != s2[i]) {
                ans++;
                turn(i);
            }
        }

        System.out.println(ans);

    }

    public static void turn(int u) {
        s1[u] = s1[u] == '*' ? 'o' : '*';
        s1[u + 1] = s1[u + 1] == '*' ? 'o' : '*';
    }
}

http://www.niftyadmin.cn/n/94637.html

相关文章

劳保防护用品穿戴检测 python

劳保防护用品穿戴检测 python

劳保防护用品穿戴检测算法通过pythonOpencv深度学习技术&#xff0c;劳保防护用品穿戴检测算法对现场人员防护穿戴用品进行全天候检测&#xff0c;当检测到未按照要求进行穿戴&#xff0c;立即对现场违规人员进行抓拍。Python是一种由Guido van Rossum开发的通用编程语言&#…
阅读更多...
C++模板元编程记录

C++模板元编程记录

C模板元编程基本技巧 C模板元编程是一种典型的函数式编程&#xff0c;核心是函数。不同于C程序中定义与使用的函数。 更接近数学意义上的函数。 constexpr int fun(int a){return a 1;}constexpr为C11关键字&#xff0c;表明该函数可在编译期调用&#xff0c;是一个元函数。…
阅读更多...
git实战技巧-本地刚做出的修改、暂存和提交如何进行撤销

git实战技巧-本地刚做出的修改、暂存和提交如何进行撤销

1、解决思路工作区和暂存区内容的撤销&#xff0c;直接按照对应命令或者IDEA界面完成操作就行。对于已提交的撤销回滚建议如下&#xff1a;1. 代码如果仅仅是回撤到指定版本&#xff0c;该版本之上的更新是不需要的&#xff0c;选择Hard模式。2. 代码回撤到指定版本时&#xff…
阅读更多...
IP、MAC和端口号——网络通信中确认身份信息的三要素

IP、MAC和端口号——网络通信中确认身份信息的三要素

目录 &#x1f30f; IP地址 &#x1f30f; MAC地址 &#x1f30f; 端口号 IP、MAC和端口号——网络通信中确认身份信息的三要素 在茫茫的互联网海洋中&#xff0c;要找到一台计算机非常不容易&#xff0c;有三个要素必须具备&#xff0c;它们分别是 IP 地址、MAC 地址和端口…
阅读更多...
小米/红米手机数据恢复：从小米手机恢复已删除的数据

小米/红米手机数据恢复：从小米手机恢复已删除的数据

如果您不小心删除了小米手机上的数据&#xff0c;后来发现您需要它&#xff0c;那么本文适合您。我将向您介绍一些最可靠的小米恢复方法&#xff0c;以将您的数据恢复到您的设备上。无论您是否有备份&#xff0c;都可以处理。让我们开始吧&#xff01; 小米数据恢复 - 如何做&a…
阅读更多...
【蓝桥集训】第七天——并查集

【蓝桥集训】第七天——并查集

作者&#xff1a;指针不指南吗 专栏&#xff1a;Acwing 蓝桥集训每日一题 &#x1f43e;或许会很慢&#xff0c;但是不可以停下来&#x1f43e; 文章目录1.亲戚2.合并集合3.连通块中点的数量有关并查集的知识学习可以移步至—— 【算法】——并查集1.亲戚 或许你并不知道&#…
阅读更多...
【架构师】零基础到精通——架构演进

【架构师】零基础到精通——架构演进

博客昵称&#xff1a;架构师Cool 最喜欢的座右铭&#xff1a;一以贯之的努力&#xff0c;不得懈怠的人生。 作者简介&#xff1a;一名Coder&#xff0c;软件设计师/鸿蒙高级工程师认证&#xff0c;在备战高级架构师/系统分析师&#xff0c;欢迎关注小弟&#xff01; 博主小留言…
阅读更多...
微服务架构下路由、多活、灰度、限流的探索与挑战

微服务架构下路由、多活、灰度、限流的探索与挑战

导语 2022腾讯全球数字生态大会已圆满落幕&#xff0c;大会以“数实创新、产业共进”为主题&#xff0c;聚焦数实融合&#xff0c;探索以全真互联的数字技术助力实体经济高质量发展。大会设有29个产品技术主题专场、18个行业主题专场和6个生态主题专场&#xff0c;各业务负责人…
阅读更多...
最新文章

Copyright @ 2022~2023